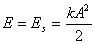Opis ruchu drgającego (prostego - bez oporów)
1) Do opisu ruchu drgającego używa się pojęć:
A) położenie równowagi
B) wychylenie i amplituda
C) okres i częśtotliwość ruchu
D) prędkość
E) przyspieszenie i siła
F) energia i przemiany energii
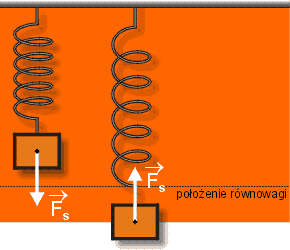
A: Położenie równowagi odpowiada stanowi ciała, w którym siły działające na ciało równoważą się (przykłady na rysunku).
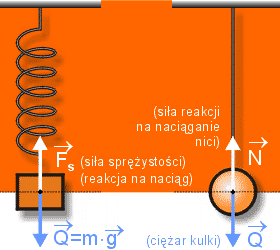
B: Wychylenie (x), to odległość ciała (punktu) drgającego od położenia równowagi. Jest ono zmienne (okresowo) w czasie.
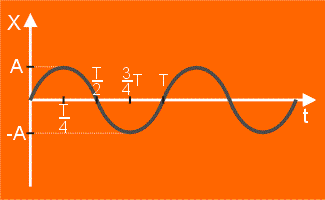
Zależność (położenia) wychylenia od czasu obrazuje poniższy wykres. Jego przebieg jest podobny do wykresu sin a, a różni się od niego wartościami maksymalnymi.
Ajest największym możliwym wychyleniem. Największe wychylenie ciała z położenia równowagi nazywamy amplitudą.
xmax = A
gdzie a to tzw. faza ruchu i 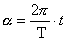 czyli
czyli 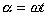 (w - prędkość kątowa), a T to okres drgań, np. gdy
(w - prędkość kątowa), a T to okres drgań, np. gdy 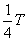 to
to 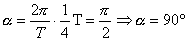 i
i 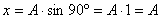
C: Okres (T) i częstotliwość (f) drgań
Okres, to czas powtarzalności. Jest to czas w którym ciało (punkt) wykona jedno pełne drganie (czyli odbędzie ruch np. od położenia równowagi do maksymalnego wychylenia, zawróci, przejdzie przez położenia równowagi do maksymalnego wychylenia w drugą stronę znów zawróci i dojdzie do położenia równowagi). Okres drgań oznaczamy literą T i wyrażamy w jednostkach czasu czyli sekundach. W czasie 1T ciało przebywa drogę równą 4A.
Odwrotność okresu 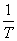 jest miarą częstotliwości drgań.
jest miarą częstotliwości drgań.
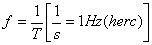
Częstotliwość to liczba drgań wykonanych w czasie jednej sekundy. Okres drgań (i częstotliwości) zależy od właściwości sprężyny do której jest doczepiony obciążnik.
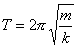
m - masa drgającą ciała (punktu), a k - współczynnik sprężystości sprężyny
D: Prędkość
Prędkość ciała (punktu) drgającego nie jest stała w czasie. Ruch drgający jest ruchem niejednostajnie opóźnionym przy wzroście wychylenia, a jednocześnie przyspieszonym przy zmniejszaniu się wychylenia. Gdy wychylenie wynosi zero(ciało przechodzi przez położenie równowagi) prędkość wynosi 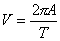 jest ona maksymalna. Gdy wychylenie jest maksymalne (A) prędkość wynosi zero (moment zawracania).
jest ona maksymalna. Gdy wychylenie jest maksymalne (A) prędkość wynosi zero (moment zawracania).
Zależność prędkości od czasu przedstawia wykres. Przypomina on przebieg zmienności funkcji 
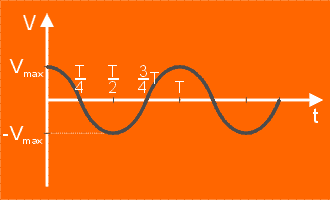
W dowolnym momencie trwania ruchu prędkość ciała drgającego wynosi: 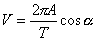 gdzie
gdzie 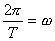 a faza
a faza 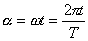 np.:
np.:
gdy 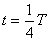 to
to 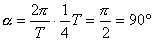 i
i 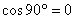 zatem V =0
zatem V =0
E: Przyspieszenie i siła
Ruch drgający nie jest jednostajnie zmienny, więc ciało drgające doznaje przyspieszenia (a) zmiennego w czasie. Przyspieszenie jest proporcjonalne do wychylenia (w tych samych momentach = a = 0 gdy x = 0 i a = a max gdy x = A), ale zwrot przyspieszenia jest przeciwny do wychylenia. Przyspieszenie jest w każdym momencie ruchu zwrócone w stronę położenia równowagi.
Przyspieszenie punktu drgającego można obliczyć z równania: 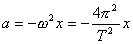
Przyspieszenie jest skutkiem działania siły sprężystości (siły dążącej do przywrócenia stanu równowagi). Tę siłę wyrażamy na podtawie II zasady dynamiki: 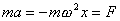
Jest ona proporcjonalna do wychylenia (gdy x rośnie, to F też rośnie) i zwrócona przeciwnie do wychylenia (zawsze do położenia równowagi).
Wyrażenie: mw2 = k jest współczynnikiem sprężystości, więc 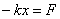
F: Energia i jej przemiany
Ciała poruszające się posiadają energię kinetyczną, zatem punkt drgający posiada energię kinetyczną, której wartość: 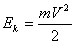
Energia kinetyczna zmienia się w czasie, gdyż prędkość ciała nie jest stała. Gdy prędkość ciała maleje, rośnie jego wychylenie i energia kinetyczna ulega przemianie w energię potencjalną (sprężystości): 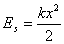
W dowolnym momencie trwania ruchu energia jest równa sumie energii kinetycznej i potencjalnej ma ona wartość: 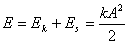
Ponieważ k (współczynnik sprężystości) i A (amplituda drgań) są dla danego ciała stałe więc energia ciała drgającego jest stała. Ulega ona przemianie tzn. Ek zamienia się w Es i na odwrót Es zamienia się w Ek.
Gdy x = 0, v = vmax i ciało ma 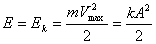 ; gdy x = A, ciało ma v = 0 i
; gdy x = A, ciało ma v = 0 i 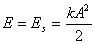
Darmowy hosting zapewnia PRV.PL


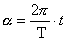 czyli
czyli 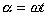 (w - prędkość kątowa), a T to okres drgań, np. gdy
(w - prędkość kątowa), a T to okres drgań, np. gdy 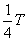 to
to 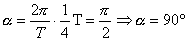 i
i 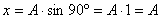

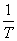 jest miarą częstotliwości drgań.
jest miarą częstotliwości drgań.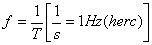
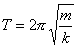
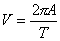 jest ona maksymalna. Gdy wychylenie jest maksymalne (A) prędkość wynosi zero (moment zawracania).
jest ona maksymalna. Gdy wychylenie jest maksymalne (A) prędkość wynosi zero (moment zawracania).

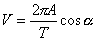 gdzie
gdzie 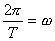 a faza
a faza 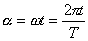 np.:
np.: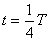 to
to 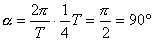 i
i 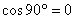 zatem V =0
zatem V =0 
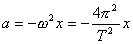
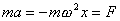
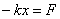
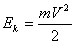
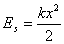
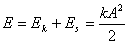
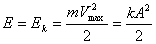 ; gdy x = A, ciało ma v = 0 i
; gdy x = A, ciało ma v = 0 i